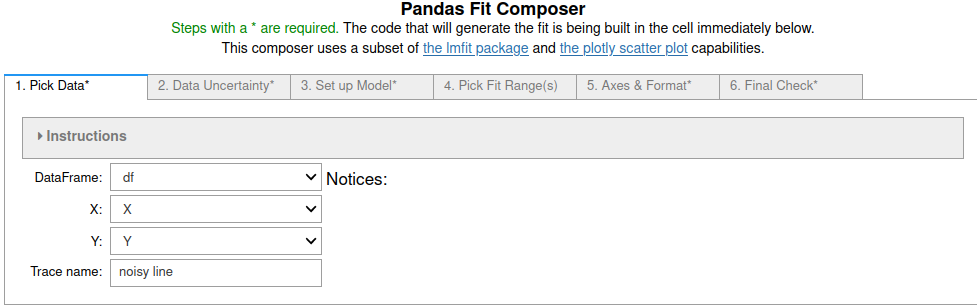
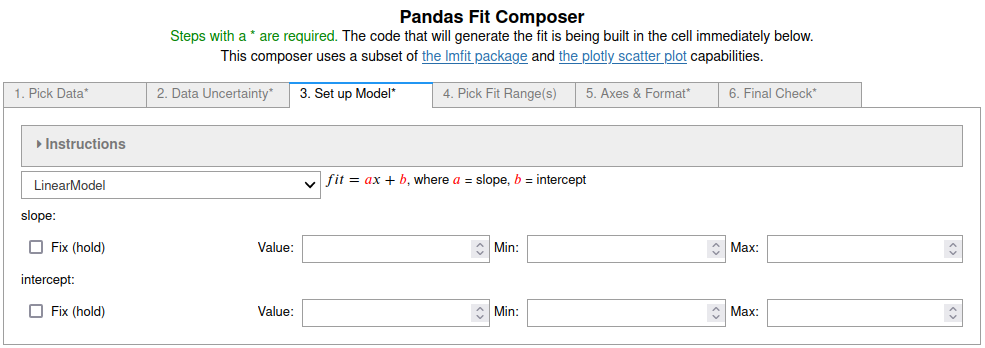
Linear fits using fit_pandas_GUI()¶

You can try this notebook live by lauching it in Binder.This can take a while to launch, be patient. Binder.

First we import pandas, numpy and pandas_GUI and then create a noisy line to fit.

In [1]:
import pandas as pd
import numpy as np
from pandas_GUI import *
df = pd.DataFrame({'X':[i/10 for i in range(-20,20)]})
df['Y'] = df['X']*2 - 0.1 + np.random.default_rng().normal(0,0.3,40)

Then make a quick plot using plot_pandas_GUI() to see what the data looks like. See the Pandas GUI Website for examples and documentation on using the plotting GUI.

In [2]:
# CODE BLOCK generated using plot_pandas_GUI().
# See https://jupyterphysscilab.github.io/jupyter_Pandas_GUI.
from plotly import graph_objects as go
Figure_1 = go.FigureWidget(layout_template="simple_white")

# Trace declaration(s) and trace formatting
scat = go.Scatter(x = df['X'], y = df['Y'],
        mode = 'markers', name = 'Y',)
Figure_1.add_trace(scat)

# Axes labels
Figure_1.update_xaxes(title= 'X', mirror = True)
Figure_1.update_yaxes(title= 'Y', mirror = True)

# Plot formatting
Figure_1.update_layout(title = 'Figure_1', template = 'simple_white', autosize=True)
Figure_1.show(config = {'toImageButtonOptions': {'format': 'svg'}})

Figure 1: Plot of the noisy linear data. Since the noise is generated using a normal distribution from a random number generator the data will look different each time the notebook is restarted and run.

Example 1: Basic linear fit¶

The fit was done by running the command fit_pandas_GUI() in an empty code cell.

1. On the first tab¶

the data set, which columns contained the X- and Y-data and a name for the trace were chosen.

Fit_tab_1

2. On the second tab¶

the the default 'none' value was kept for uncertainties.

Fit_tab_2

3. On the third tab¶

the linear model was chosen and all the boxes were left in their default state.

Fit_tab_3

4. The fourth tab was skipped¶

because we fit the whole range of data.

5. On the fifth tab¶

labels for the X and Y axis were input and the Display Mirror Axes box was checked.

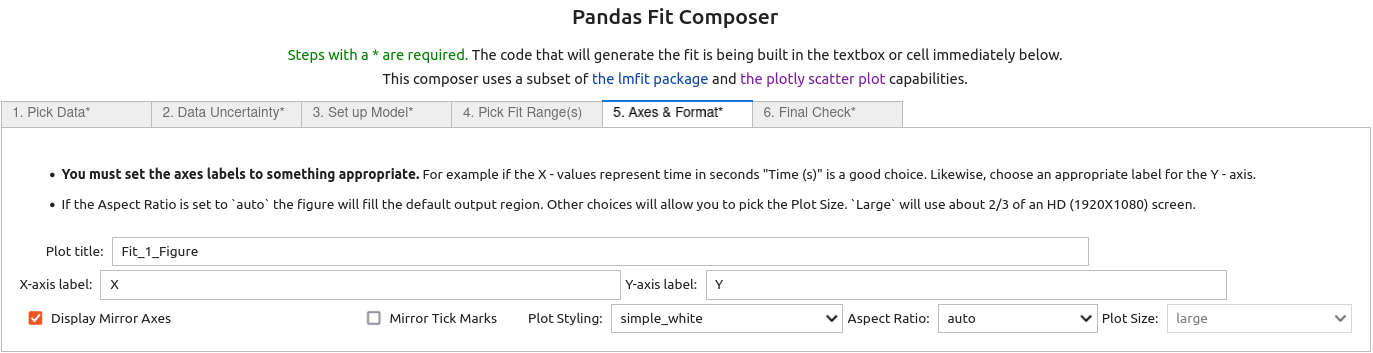
Fit_tab_5

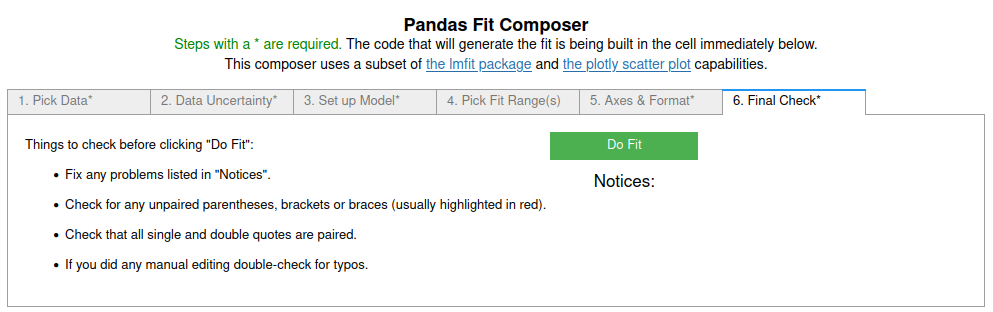
6. On the last (sixth) tab¶

the final checks were done and then the 'Do Fit' button was clicked, closing the GUI and running the code in the cell below to perform the fit and display the results.

Fit_tab_6

In [3]:
# CODE BLOCK generated using fit_pandas_GUI().
# See https://jupyterphysscilab.github.io/jupyter_Pandas_GUI.
# Integers wrapped in `int()` to avoid having them cast 
# as other types by interactive preparsers. 
# Imports (no effect if already imported)
import numpy as np
import lmfit as lmfit
import round_using_error as rue
import copy as copy
from plotly import graph_objects as go
from IPython.display import HTML, Math

# Define data and trace name
Xvals = df["X"]
Yvals = df["Y"]
tracename = "Noisy Linear Data"

# Define error (uncertainty)
Yerr = df["Y"]*0.0 + 1.0

# Define the fit model, initial guesses, and constraints
fitmod = lmfit.models.LinearModel()
fitmod.set_param_hint("slope", vary = True, value = 0.0)
fitmod.set_param_hint("intercept", vary = True, value = 0.0)

# Do fit
Fit_1 = fitmod.fit(Yvals, x=Xvals, weights = 1/Yerr, scale_covar = True, nan_policy = "omit")

# Calculate residuals (data - fit) because lmfit
#  does not calculate for all points under all conditions
resid = []
# explicit int(0) below avoids collisions with some preparsers.
for i in range(int(0),len(Fit_1.data)):
    resid.append(Fit_1.data[i]-Fit_1.best_fit[i])

# Plot Results
# explicit int(..) below avoids collisions with some preparsers.
Fit_1_Figure = go.FigureWidget(layout_template="simple_white")
Fit_1_Figure.update_layout(title = "Fit_1_Figure",autosize=True)
Fit_1_Figure.set_subplots(rows=int(2), cols=int(1), row_heights=[0.2,0.8], shared_xaxes=True)
scat = go.Scatter(y=resid,x=Xvals, mode="markers",name = "residuals")
Fit_1_Figure.update_yaxes(title = "Residuals", row=int(1), col=int(1), zeroline=True, zerolinecolor = "lightgrey", mirror = True)
Fit_1_Figure.update_xaxes(row=int(1), col=int(1), mirror = True)
Fit_1_Figure.add_trace(scat,col=int(1),row=int(1))
scat = go.Scatter(x=Xvals, y=Yvals, mode="markers", name=tracename)
Fit_1_Figure.add_trace(scat, col=int(1), row=int(2))
Fit_1_Figure.update_yaxes(title = "Y", row=int(2), col=int(1), mirror = True)
Fit_1_Figure.update_xaxes(title = "X", row=int(2), col=int(1), mirror = True)
scat = go.Scatter(y=Fit_1.best_fit,x=Xvals, mode="lines", name="fit", line_color = "black", line_dash="solid")
Fit_1_Figure.add_trace(scat,col=int(1),row=int(2))
Fit_1_Figure.show(config = {'toImageButtonOptions': {'format': 'svg'}})

# Display best fit equation
slopestr = ''
interceptstr = ''
for k in Fit_1.params.keys():
    if Fit_1.params[k].vary:
        paramstr = r'({\color{red}{'+rue.latex_rndwitherr(Fit_1.params[k].value,
                                       Fit_1.params[k].stderr,
                                       errdig=int(1),
                                       lowmag=-int(3))+'}})'
    else:
        paramstr = r'{\color{blue}{'+str(Fit_1.params[k].value,
                                       )+'}}'
    if k == 'slope':
        slopestr = paramstr
    if k == 'intercept' and Fit_1.params[k].value != 0:
        interceptstr = ' + ' + paramstr
fitstr = r'$fit = '+slopestr + 'x' + interceptstr + '$'
captionstr = r'<p>Use the command <code>Fit_1</code> as the last line of a code cell for more details.</p>'
display(Math(fitstr))
display(HTML(captionstr))
$\displaystyle fit = ({\color{red}{1.96\pm0.03}})x + ({\color{red}{-0.06\pm0.03}})$

Use the command Fit_1 as the last line of a code cell for more details.

Figure 2: The results of fitting the noisy linear data to a line using default settings. Alternative formatting of line styles, markers, etc... can be accessed by editing the code produced by the GUI. Overall plot styling can be adjusted on tab 5.

Example 2: Linear fit with known errors in the measurements¶

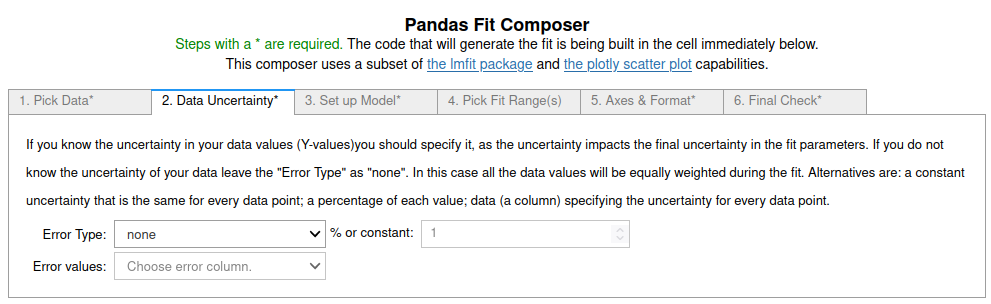
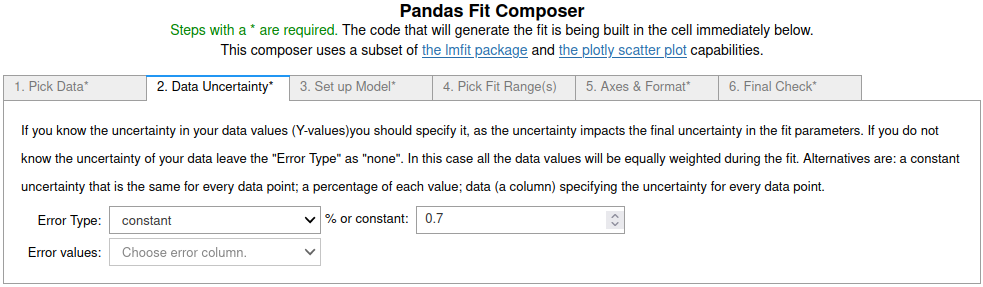
Errors can be a constant value (same on all data points), a percentage of each value or a value provided in a column of the pandas dataframe. For this example we will use a constant that is a little bigger than the random error used to generate the data. This causes the uncertainties in the fit parameters to increase.

The only change from the steps in example 1 is on tab 2 where the Error Type is changed to "constant" and the value in the % or constant box is set to "0.7". It is important to click outside this box to register the updated value.

Fit_line_with_errors_tab3

In [4]:
# CODE BLOCK generated using fit_pandas_GUI().
# See https://jupyterphysscilab.github.io/jupyter_Pandas_GUI.
# Integers wrapped in `int()` to avoid having them cast 
# as other types by interactive preparsers. 
# Imports (no effect if already imported)
import numpy as np
import lmfit as lmfit
import round_using_error as rue
import copy as copy
from plotly import graph_objects as go
from IPython.display import HTML, Math

# Define data and trace name
Xvals = df["X"]
Yvals = df["Y"]
tracename = "Noisy Linear Data"

# Define error (uncertainty)
Yerr = df["Y"]*0.0 + 1.0

# Define the fit model, initial guesses, and constraints
fitmod = lmfit.models.LinearModel()
fitmod.set_param_hint("slope", vary = True, value = 0.0)
fitmod.set_param_hint("intercept", vary = True, value = 0.0)

# Do fit
Fit_2 = fitmod.fit(Yvals, x=Xvals, weights = 1/Yerr, scale_covar = False, nan_policy = "omit")

# Calculate residuals (data - fit) because lmfit
#  does not calculate for all points under all conditions
resid = []
# explicit int(0) below avoids collisions with some preparsers.
for i in range(int(0),len(Fit_2.data)):
    resid.append(Fit_2.data[i]-Fit_2.best_fit[i])

# Plot Results
# explicit int(..) below avoids collisions with some preparsers.
Fit_2_Figure = go.FigureWidget(layout_template="simple_white")
Fit_2_Figure.update_layout(title = "Fit_2_Figure",autosize=True)
Fit_2_Figure.set_subplots(rows=int(2), cols=int(1), row_heights=[0.2,0.8], shared_xaxes=True)
scat = go.Scatter(y=resid,x=Xvals, mode="markers",name = "residuals", error_y_type="data", error_y_array=Yerr)
Fit_2_Figure.update_yaxes(title = "Residuals", row=int(1), col=int(1), zeroline=True, zerolinecolor = "lightgrey", mirror = True)
Fit_2_Figure.update_xaxes(row=int(1), col=int(1), mirror = True)
Fit_2_Figure.add_trace(scat,col=int(1),row=int(1))
scat = go.Scatter(x=Xvals, y=Yvals, mode="markers", name=tracename, error_y_type="data", error_y_array=Yerr)
Fit_2_Figure.add_trace(scat, col=int(1), row=int(2))
Fit_2_Figure.update_yaxes(title = "Y", row=int(2), col=int(1), mirror = True)
Fit_2_Figure.update_xaxes(title = "X", row=int(2), col=int(1), mirror = True)
scat = go.Scatter(y=Fit_2.best_fit,x=Xvals, mode="lines", name="fit", line_color = "black", line_dash="solid")
Fit_2_Figure.add_trace(scat,col=int(1),row=int(2))
Fit_2_Figure.show(config = {'toImageButtonOptions': {'format': 'svg'}})

# Display best fit equation
slopestr = ''
interceptstr = ''
for k in Fit_2.params.keys():
    if Fit_2.params[k].vary:
        paramstr = r'({\color{red}{'+rue.latex_rndwitherr(Fit_2.params[k].value,
                                       Fit_2.params[k].stderr,
                                       errdig=int(1),
                                       lowmag=-int(3))+'}})'
    else:
        paramstr = r'{\color{blue}{'+str(Fit_2.params[k].value,
                                       )+'}}'
    if k == 'slope':
        slopestr = paramstr
    if k == 'intercept' and Fit_2.params[k].value != 0:
        interceptstr = ' + ' + paramstr
fitstr = r'$fit = '+slopestr + 'x' + interceptstr + '$'
captionstr = r'<p>Use the command <code>Fit_2</code> as the last line of a code cell for more details.</p>'
display(Math(fitstr))
display(HTML(captionstr))
$\displaystyle fit = ({\color{red}{2.0\pm0.1}})x + ({\color{red}{-0.06\pm0.16}})$

Use the command Fit_2 as the last line of a code cell for more details.

Figure 3: Results of fitting the noisy line while accounting for assigned errors in the values. This changes the uncertainty in the fitted parameters. In this case the y-intercept cannot really be distinguished from zero. Note: if the data set is dense the default display of error bars can make it hard to see what is happening. The error bars can be removed, while still accounting for them in the fit, by deleting error_y_type="data", error_y_array=Yerr where they appear in the scat= statements.

Example 3: Fit to a portion of the data¶

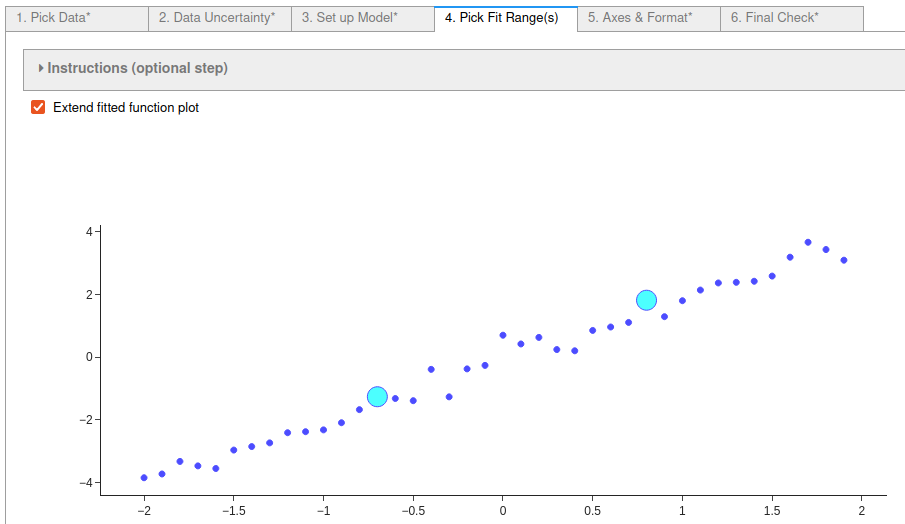
A range or multiple ranges of the data set to fit may be selected using the optional tab 4. Consecutive pairs of selected points starting with the lowest data index number define each range. Points can be deselected by holding down the ctrl key while clicking on a point.

For this example we have selected a range in the middle of the plot and extended the fit so that the fit and residuals are extrapolated across the whole data range as shown in the image below.

Fit_line_range

In [6]:
# CODE BLOCK generated using fit_pandas_GUI().
# See https://jupyterphysscilab.github.io/jupyter_Pandas_GUI.
# Integers wrapped in `int()` to avoid having them cast 
# as other types by interactive preparsers. 
# Imports (no effect if already imported)
import numpy as np
import lmfit as lmfit
import round_using_error as rue
import copy as copy
from plotly import graph_objects as go
from IPython.display import HTML, Math

# Define data and trace name
Xvals = df["X"]
Yvals = df["Y"]
tracename = "Noisy Linear Data"

# Define error (uncertainty)
Yerr = df["Y"]*0.0 + 1.0

# Define the fit model, initial guesses, and constraints
fitmod = lmfit.models.LinearModel()
fitmod.set_param_hint("slope", vary = True, value = 0.0)
fitmod.set_param_hint("intercept", vary = True, value = 0.0)

# Define fit ranges
Yfiterr = copy.deepcopy(Yerr) # ranges not to fit = np.inf
Xfitdata = copy.deepcopy(Xvals) # ranges where fit not displayed = np.nan
Yfiterr[int(0):int(13)] = np.inf
Xfitdata[int(0):int(13)] = np.nan
Yfiterr[int(30):int(40)] = np.inf
Xfitdata[int(30):int(40)] = np.nan

# Do fit
Fit_3 = fitmod.fit(Yvals, x=Xvals, weights = 1/Yfiterr, scale_covar = True, nan_policy = "omit")

# Calculate residuals (data - fit) because lmfit
#  does not calculate for all points under all conditions
resid = []
# explicit int(0) below avoids collisions with some preparsers.
for i in range(int(0),len(Fit_3.data)):
    resid.append(Fit_3.data[i]-Fit_3.best_fit[i])

# Plot Results
# explicit int(..) below avoids collisions with some preparsers.
Fit_3_Figure = go.FigureWidget(layout_template="simple_white")
Fit_3_Figure.update_layout(title = "Fit_3_Figure",autosize=True)
Fit_3_Figure.set_subplots(rows=int(2), cols=int(1), row_heights=[0.2,0.8], shared_xaxes=True)
scat = go.Scatter(y=resid,x=Xvals, mode="markers",name = "residuals")
Fit_3_Figure.update_yaxes(title = "Residuals", row=int(1), col=int(1), zeroline=True, zerolinecolor = "lightgrey", mirror = True)
Fit_3_Figure.update_xaxes(row=int(1), col=int(1), mirror = True)
Fit_3_Figure.add_trace(scat,col=int(1),row=int(1))
scat = go.Scatter(x=Xvals, y=Yvals, mode="markers", name=tracename)
Fit_3_Figure.add_trace(scat, col=int(1), row=int(2))
Fit_3_Figure.update_yaxes(title = "Y", row=int(2), col=int(1), mirror = True)
Fit_3_Figure.update_xaxes(title = "X", row=int(2), col=int(1), mirror = True)
scat = go.Scatter(y=Fit_3.best_fit, x=Xvals, mode="lines", line_color = "black", name="extrapolated",line_dash="dash")
Fit_3_Figure.add_trace(scat, col=int(1), row=int(2))
scat = go.Scatter(y=Fit_3.best_fit,x=Xfitdata, mode="lines", name="fit", line_color = "black", line_dash="solid")
Fit_3_Figure.add_trace(scat,col=int(1),row=int(2))
Fit_3_Figure.show(config = {'toImageButtonOptions': {'format': 'svg'}})

# Display best fit equation
slopestr = ''
interceptstr = ''
for k in Fit_3.params.keys():
    if Fit_3.params[k].vary:
        paramstr = r'({\color{red}{'+rue.latex_rndwitherr(Fit_3.params[k].value,
                                       Fit_3.params[k].stderr,
                                       errdig=int(1),
                                       lowmag=-int(3))+'}})'
    else:
        paramstr = r'{\color{blue}{'+str(Fit_3.params[k].value,
                                       )+'}}'
    if k == 'slope':
        slopestr = paramstr
    if k == 'intercept' and Fit_3.params[k].value != 0:
        interceptstr = ' + ' + paramstr
fitstr = r'$fit = '+slopestr + 'x' + interceptstr + '$'
captionstr = r'<p>Use the command <code>Fit_3</code> as the last line of a code cell for more details.</p>'
display(Math(fitstr))
display(HTML(captionstr))
$\displaystyle fit = ({\color{red}{1.97\pm0.06}})x + ({\color{red}{-0.04\pm0.03}})$

Use the command Fit_3 as the last line of a code cell for more details.

Figure 4: Fit to only the region with the solid fit line. If the Extend fitted function plot box had not been checked the dashed line and residuals outside the fit region would not be plotted.

Learn More¶

In addition to trying it below if this is a live notebook, you can look at the other examples listed in the Pandas GUI website.

Try It¶

If you are running this notebook live in binder you can try it here by running the first cell to import the tools and create the data. Then run the cell below to create the GUI. Note: You may want to expand the collapsed instructions to learn more about each tab.

In [ ]:
fit_pandas_GUI()